파이토치(PyTorch) tutorial_2

☞    문서의 내용은 가장 하단 참고문헌 및 사이트를 참고하여 필자가 보기 쉽도록 정리한 내용입니다.

☞    틀린 내용 및 저작권 관련 문의가 있는 경우 문의하시면 수정 및 삭제 조치하겠습니다.

---

자동 미분 (Autograd : automatic differentiation)

autograd package는 Tensor의 모든 연산에 대해 자동 미분을 제공한다. define-by-run framework로, 코드를 어떻게 작성하여 실행하느냐에 따라 역전파가 정의된다는 뜻이며, 역전파는 학습 과정의 매 단계마다 달라진다.

출처 : Complex neural networks made easy by Chainer

 

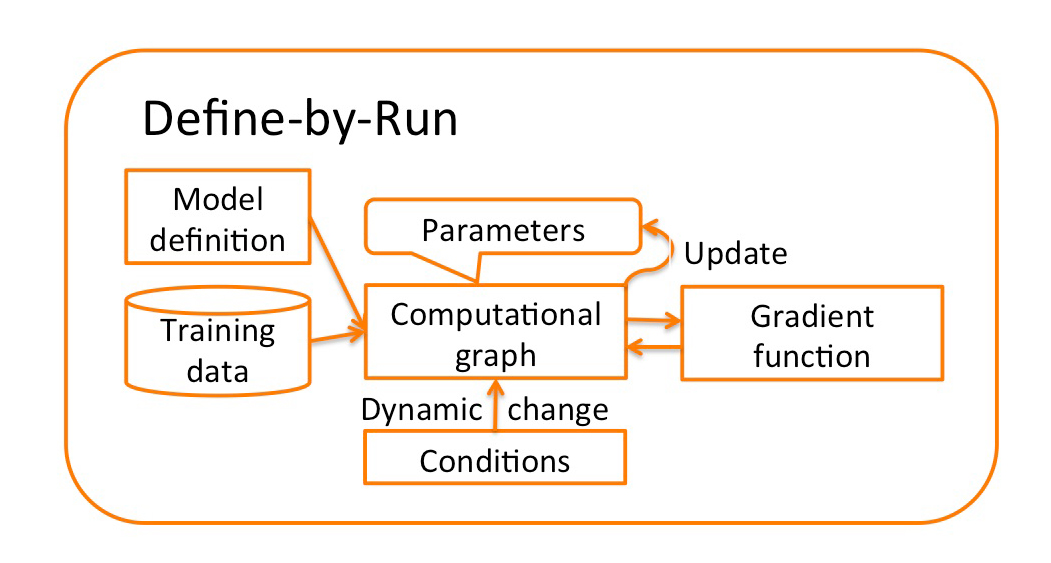
torch.Tensor는 package에서 중심이 되는 class이다.  .requires_grad 속성을 True로 설정하면, 그 tensor에서 이뤄진 모든 연산들을 추적한다. 계산이 완료된 후 .backward()를 호출하여 모든 변화도(gradient)를 자동으로 계산할 수 있다. 이 변화도는 .grad에 누적된다. Tensor가 기록을 추적하는 것을 중단하려면 .detach()를 호출하여 이후 연산들이 추적되는 것을 방지할 수 있다. 메모리 사용량을 줄이기 위해 코드 블럭을 with torch.no_grad():로 감싼다. 그 이유는 학습된 파라미터 값을 평가하는 단계에서는 gradient를 계산할 필요가 없기 때문이다. 이는 모델을 평가할 때 도움이된다.  

 

---

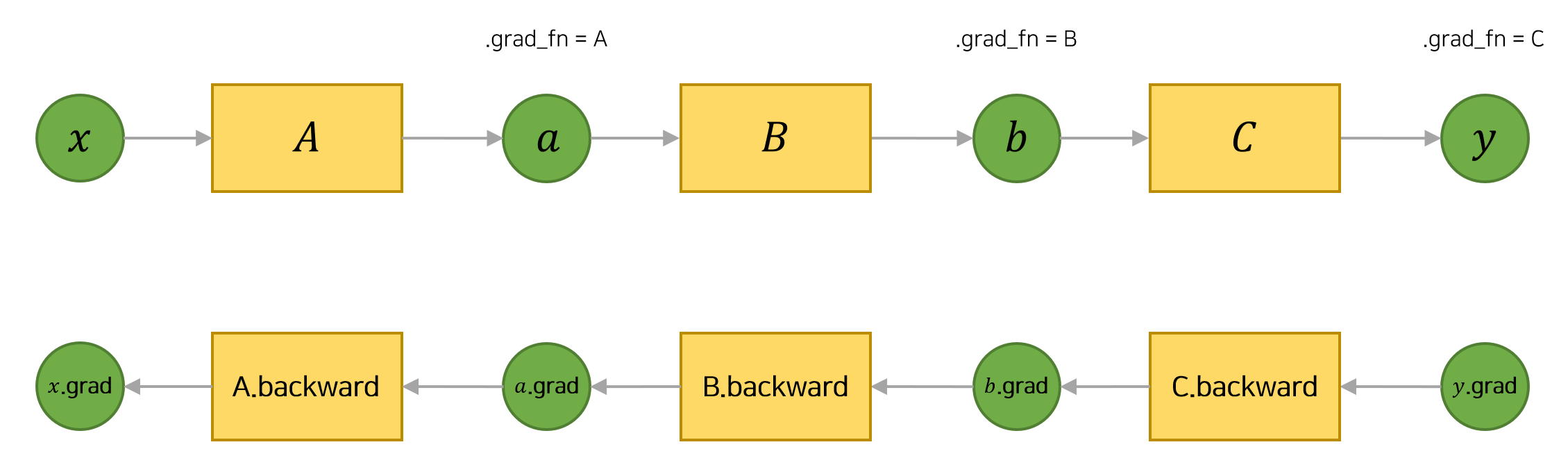
Autograd에서 중요한 class가 Function class이다. Tensor와 function은 서로 연결되어 있으며, 모든 연산 과정을 부호화(encode)하여 순환하지 않는 그래프(acyclic graph)를 생성한다. 

 

acyclic graph

 

각 tensor는 .grad_fn속성을 갖고 있는데, 이는 Tensor를 생성한 Function을 참조하고 있다. (단, 사용자가 만든 Tensor는 예외로, 이 때 grad_fn은 None이다.) 도함수를 계산하기 위해서는 Tensor의 .backward()를 호출하면 된다. 만약 Tensor가 스칼라(scalar)인 경우에는 backward에 인자값을 지정해줄 필요가 없다. 하지만 여러개의 요소를 갖고 있을 때는 tensor를 지정해줘야한다.

 

 

---

tensor를 생성하고 requires_grad=True를 설정하여 연산을 기록한다.

import torch

x = torch.ones(2, 2, requires_grad=True)
print(x)

#out :
#tensor([[1., 1.],
#        [1., 1.]], requires_grad=True)

 

tensor에 연산을 수행한다.

y = x + 2
print(y)

#out : 
#tensor([[3., 3.],
#        [3., 3.]], grad_fn=<AddBackward0>)

 

y는 연산의 결과로 생성된 것이므로 grad_fn을 갖는다.

print(y.grad_fn)

#out :
#<AddBackward0 object at 0x7f843916f0f0>

 

y에 다른 연산을 수행한다.

z = y * y * 3
out = z.mean()

print(z, out)

#out :
#tensor([[27., 27.],
#       [27., 27.]], grad_fn=<MulBackward0>) tensor(27., grad_fn=<MeanBackward0>)

 

.requires_grad_( ... )는 기존 Tensor의 requires_grad 값을 바꿔치기 (in-place)하여 변경한다. 입력값이 지정되지 않으면 기본값은 False이다.

a = torch.randn(2, 2)
a = ((a * 3) / (a - 1))
print(a.requires_grad)
a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)

#Out:
#False
#True
#<SumBackward0 object at 0x7f843916f470>

 

---

변화도(Gradient)

이제 역전파(backprop)를 해보자 out은 하나의 스칼라 값만 갖고 있기 때문에, out.backward()는 out.backward(torch.tensor(1.))과 동일하다.

out.backward()
print(x.grad)

#out:
#tensor([[4.5000, 4.5000],
#        [4.5000, 4.5000]])

 

4.5로 이루어진 행렬을 확인할 수 있다. out을 Tensor "o"라고 하면, 다음과 같이 구할 수 있다.

 

$o = \frac{1}{4} \sum_i z_i$ 이고

$z_i = 3(x_i + 2)^2$이므로

$z_i = 3(x_i + 2)^2z_i \rvert _{x_i=1} = 27$이다.

따라서 $\frac{\partial o}{\partial x_i} = \frac{2}{3}(x_i + 2)$ 이므로

$z_i = 3(x_i + 2)^2\frac{\partial o}{\partial x_i} \rvert _{x_i=1} = \frac{9}{2} = 4.5$이다.

 

수학적으로 벡터 함수 $\vec{y}=f(\vec{x})  $에서 $\vec{x} $에 대한 $\vec{y}$의 변화도는 야코비안 행렬(jacobian Matrix)이다 :

 

$$\begin{split}J=\left(\begin{array}{ccc}
 \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\
 \vdots & \ddots & \vdots\\
 \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}}
 \end{array}\right)\end{split}$$

 

일반적으로, torch.autograd는 벡터-야코비안 곱을 계산하는 엔진이다. 즉, 어떤 벡터 $v=\left(\begin{array}{cccc} v_{1} & v_{2} & \cdots & v_{m}\end{array}\right)^{T}$에 대해 $v^{T}\cdot J$을 연산한다.  만약 $v$가 스칼라 함수 $l=g\left(\vec{y}\right)$의 기울기인 경우, $v=\left(\begin{array}{ccc}\frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}}\end{array}\right)^{T}$이며, 연쇄법칙(chain rule)에 따라 벡터-야코비안 곱은 $\vec{x}$에대 한 $l$의 기울기가 된다 :

 

$$\begin{split}J^{T}\cdot v=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{1}}\\  \vdots & \ddots & \vdots\\ \frac{\partial y_{1}}{\partial x_{n}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\left(\begin{array}{c} \frac{\partial l}{\partial y_{1}}\\ \vdots\\ \frac{\partial l}{\partial y_{m}}  \end{array}\right)=\left(\begin{array}{c} \frac{\partial l}{\partial x_{1}}\\ \vdots\\ \frac{\partial l}{\partial x_{n}} \end{array}\right)\end{split}e$$

 

(여기서 $v^{T}\cdot J$은 $J^{T}\cdot v$를 취했을 때의 열 벡터로 취급할 수 있는 행 벡터를 갖는다.)

 

벡터 - 야코비안 곱의 이러한 특성은 스칼라가 아닌 출력을 갖는 모델에 외부 변화도를 제공(feed)하는 것을 매우 편리하게 해준다. 이제 벡터-야코비안 곱의 예제를 살펴보도록 하자.

x = torch.randn(3, requires_grad=True)

y = x * 2
while y.data.norm() < 1000:
    y = y * 2

print(y)

#out :
#tensor([-946.5160, -135.5746, -367.5571], grad_fn=<MulBackward0>)

 

이 경우 y는 더 이상 스칼라 값이 아니다. torch.autograd는 전체 야코비안을 직접 계산할수는 없지만, 벡터-야코비안 곱은 간단히 backward에 해당 벡터를 인자로 제공하여 얻을 수 있다.

v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)

print(x.grad)

#Out :
#tensor([5.1200e+01, 5.1200e+02, 5.1200e-02])

 

또한 with torch.no_grad(): 로 코드 블럭을 감싸서 autograd가 .requires_grad=True 인 Tensor들의 연산 기록을 추적하는 것을 멈출 수 있습니다.

print(x.requires_grad)
print((x ** 2).requires_grad)

with torch.no_grad():
    print((x ** 2).requires_grad)
    
#Out :
#True
#True
#False

 

또는 .detach() 를 호출하여 내용물(content)은 같지만 require_grad가 다른 새로운 Tensor를 가져옵니다:

print(x.requires_grad)
y = x.detach()
print(y.requires_grad)
print(x.eq(y).all())

#Out :
#True
#False
#tensor(True)

 

---

참고문헌

1장 파이토치란?

밑바닥부터 시작하는 딥러닝 3

Pytorch Tutorial 기본 (2) :