DeepPose: Human Pose Estimation via Deep Neural Networks

☞    문서의 내용은 가장 하단 참고문헌 및 사이트를 참고하여 필자가 보기 쉽도록 정리한 내용입니다.

☞    틀린 내용 및 저작권 관련 문의가 있는 경우 문의하시면 수정 및 삭제 조치하겠습니다.

---

DeepPose는 논문 제목에서도 알 수 있듯이 DNN 기반의 Human Pose Estimation 방법을 제안한다. Pose Estimation 분야에 최초로 DNN을 적용하여 SOTA를 달성했다. 논문은 Cascade방식의 딥러닝 회귀문제로 높은 정확도를 얻었다. 딥러닝을 classification(분류)에만 사용하였는데, Regression(회귀)문제에도 훌륭하게 적용할 수 있다는 것을 보여준 논문이다. 

 

Pose Estimation 분야에서 CNN이 적합한 이유는 다음과 같다. 첫 번째로 관절 위치 예측시에 이미지 맥락을 파악하여 예측 할 수 있다. 때문에 관절들 사이의 상관 관계를 학습 할 수 있다. 두 번째로 기존 모델들은 각 관절 별로 Feature Representation(특징검출)과 검출기 (detector)로 만든 다음, 이를 조합하는 방식이었다. 그러나 CNN을 활용하면 단일 신경망으로 모든 관절 위치를 예측할 수 있으므로 훨씬 모델이 단순해진다.

 

논문에서는 cascade방식의 Pose Estimation을 제안한다. 이러한 cascade는 joint localization의 정밀도를 높힐 수 있다. 첫 번째로 전체 이미지에 대한 초기 자세를 추정하고 고해상도의 부분 이미지를 통해 joint 예측치를 정제하는 DNN 기반의 regressor를 학습한다.

---

*캐스캐이드(cascade)란 용어는 하나의 검출기로 물체를 찾는 것이 아니라 여러개의 검출기를 순차적으로 사용하되 처음에는 간단한 검출기를 적용하고 점점 더 어려운 검출기를 적용하는 방법

---

Deep Learning Model for Pose Estimation

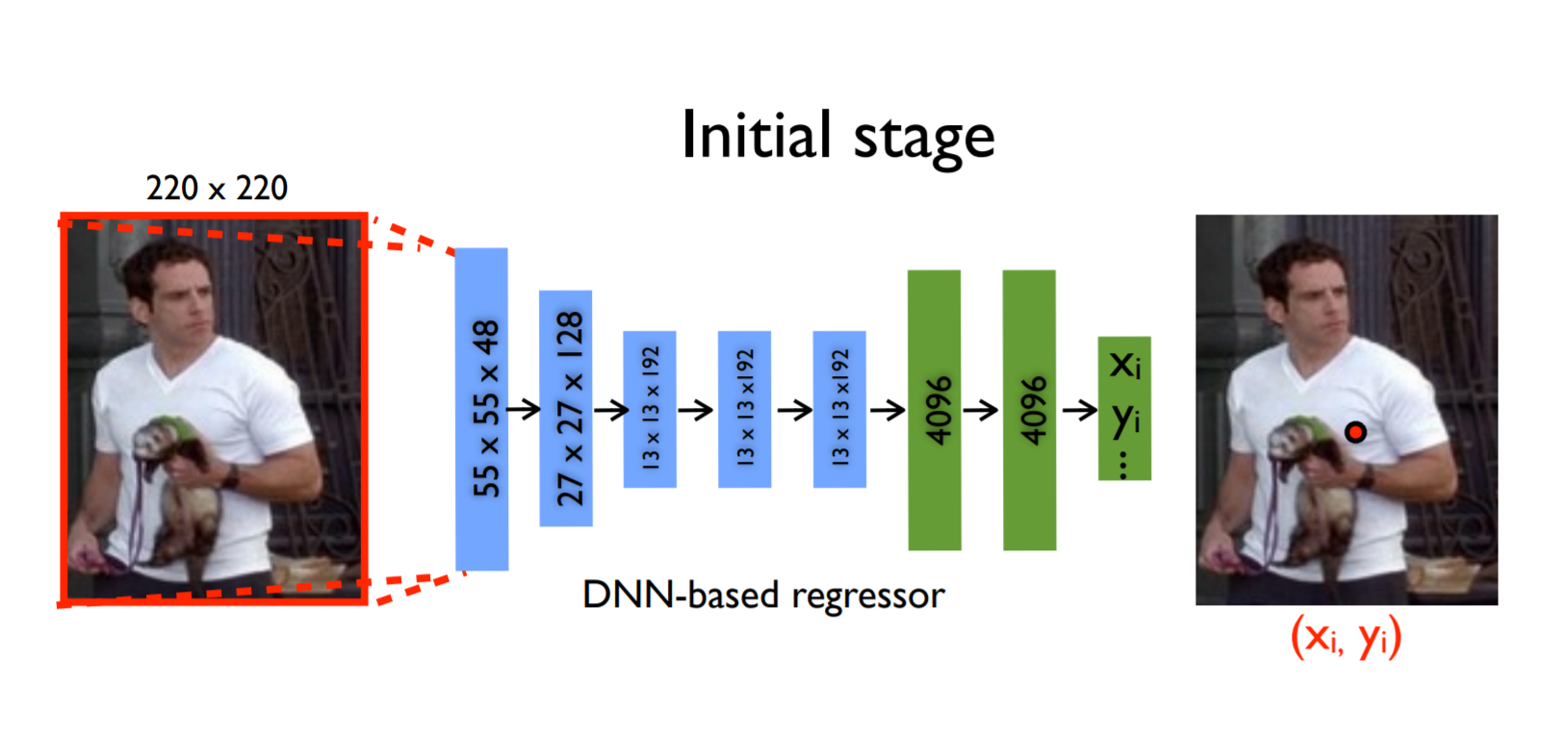
먼저 입력 이미지를 CNN에 통과시키면 k개의 관절에 대해서 예측 값을 내며 이는 총 2k 차원의 Vector(x ,y)에 해당한다. 이를 식으로 나타내면 아래와 같다.

 

x : Image data
y : Ground truth pose vector
k : 신체 관절 수
y_i : i 번째 관절의 x, y 좌표가 들어 있다.(이미지 내의 절대 좌표이다.)

 

이때 y_i의 좌표는 아래식과 같이 normalize한 N(y_i, b)로 사용되며, 이때 b는 사람의 신체에 대한 바운딩박스를 의미한다.

 

b = (b_c, B_w, B_h)
b_c : center of bounding box (BB의 중심)
b_w : width of b (BB의 너비)
b_h: height of b (BB의 높이)

 

그리고 동일한 정규화 과정을 Pose Vector 인자 모두에 적용하여 normalized pose vector를 얻는다. 아래와 같이 yi는 상자 크기로 조정되고 상자 중심으로 변환된다. 때문에 학습하기 더 편리해진다. N(y;b)는 정규화 된 Pose Vector이다. 그리고 N(x;b)는 위의 그림에서 볼 수 있는 것 처럼 Normalization Image이다.

 

 

---

*수식에 세미콜론의 의미 : 함수의 입력 파라미터 목록에 사용되는 세미콜론은 변수와 파라미터를 구분하는 역할을 한다. 세미콜론을 기준으로 앞은 입력 데이터인 변수이며 뒤쪽은 함수 내부에서 사용하는 파라미터이다. 이렇게 함수 표현에 세미콜론을 사용하여 입력 데이터와 내부 파라미터를 구분할 수 있다.   

 출처 :  YAEWAN.KIM블로그 

---

Pose Esimation as DNN-based Regression

원본 이미지 x를 Pose Vector y로 회귀하는 함수 ψ(x;θ) ∈ $R^{2k}$을 학습하고 싶다.(k : 관절 수)

원본 이미지 x 중의 관절위치 y*를 예측한다는 것은 이미지를 ψ에 넣어 Normalized Pose Vector를 얻어 이를 원래 이미지의 좌표계로 다시 변환하다는 것이므로,  y*는 아래 식과 같이 변환을 통해 절대 좌표 값으로 변환이 가능하다. (즉, 정규화된 값들을 학습하여 예측 값을 내어 이를 다시 원래의 이미지에 찍어 주려면 normalized 과정을 거꾸로 적용하면 된다. )

 

 

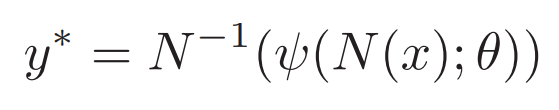
x : 입력 이미지 
φ : CNN 모델을 통과시키는 함수
θ : 학습되는 파라미터

 

입력 이미지와 파라미터를 가지고 CNN이 정규화된 예측 값을 내놓고, 이를 다시 정규화를 역으로 적용하여  관절 예측 벡터인 y*를 내놓게 된다. 이것이 위 그림에서 initialState에 해당한다. 이렇게 구한 관절 예측 값은 큰 이미지를 보고 예측한 것이라 정교함이 떨어진다는 것이 저자의 주장이다. 여기서 제안된 아이디어는 예측 좌표 주변으로 바운딩 박스를 다시 그리고, 이를 Crop하여 다시 CNN 모델을 통과시키는 Cascade 방식이다.

 

---

네트워크 구조

C : convolutional layer
LRN : local response normalization layer (요즘엔 잘 쓰이지 않고, BN(Batch Normalization)을 많이 사용함)
P : pooling layer
F : fully connected layer

 

DeepCNN의 Architecure는 AlexNet을 그대로 사용한다.(다만 최종층은 1000units가 아닌 2k units로 한다.) 첫 번째, 두 번째 Convolution 레이어는 11 x 11 , 5 x 5 필터 사이즈를, 나머지 세 번째 부터 나오는 Convolution 레이어는 3 x 3 필터 사이즈를 갖는다. 입력 이미지의 크기는 220 x 220으로 첫번째 레이어에서 stride 4가 적용된다. 활성화 함수에는 모두 ReLU를 사용했다. 

---

*LRN : Neural Networkm의 Feature에서 한 세포가 유별나게 강한 값을 가지게 된다면, 근처의 값이 약하더라도 convolution 연산을 한다면 강한 feature를 가지게 된다. 그러면 over-fitting이 잘일어나게 된다. (training dataset에만 feature가 크게 반응하니까) 그래서 어떠한 filter가 있을 때, 그 주위 혹은 같은 위치에 다른 channel의 filter들을 square-sum하여 한 filter에서만 과도하게 activate하는 것을 막음

출처 : curaai00.tistory.com/4

---

Training

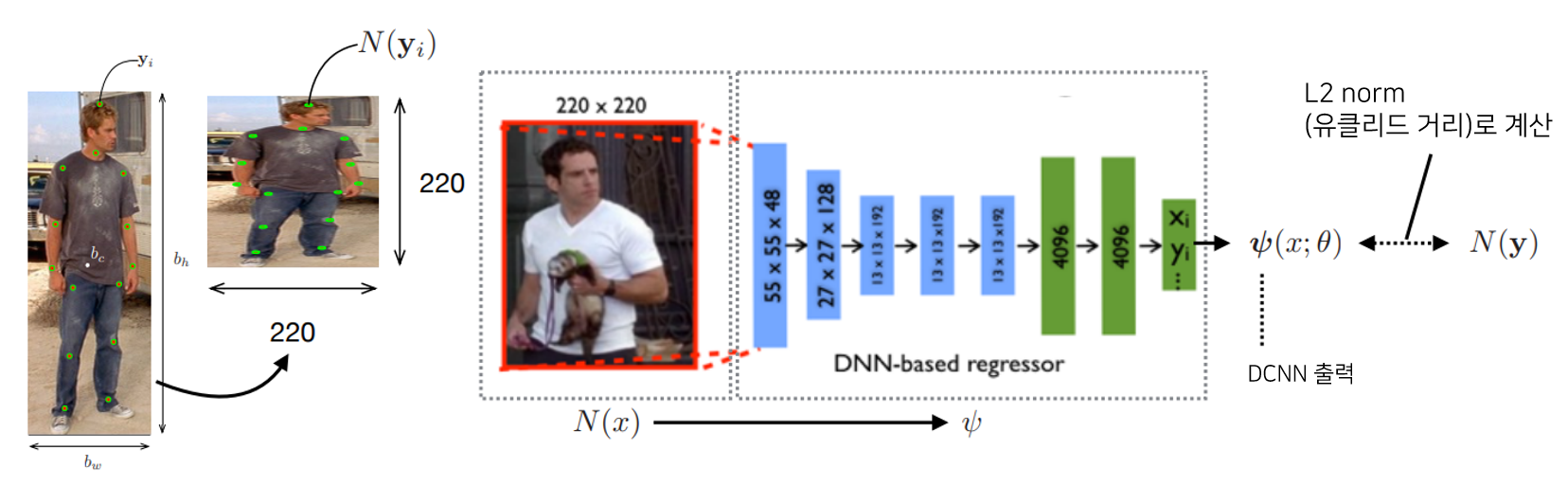
우선 데이터 셋 내의 데이터를 전부 (Normalization image N(x), Normalization pose vector N(y))로 변환해 둔다. loss function을 예측 벡터 ψ(x;θ)와 정답 벡터 N(y) 사이의 유클리드 거리로 정의한다.

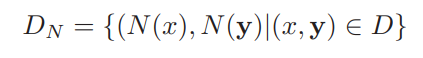
k개의 관절별 L2 norm의 합계를 전체 데이터에 걸쳐 합계한 값을 최소로 하는 DCNN의 파라미터 θ를 구한다. 그리고 θ를 mini-batched Stochastic Gradient Descent에 최적화한다.

---

*L2 Norm은 벡터 p, q의 유클리디안 거리(직선 거리)이다. 여기서 q가 원점이라면 p, q의 L2 Norm은 벡터p의 원점으로 부터의 직선 거리라고 할 수 있다. 

*arg 는 argument or a set of arguments which maximize or minimize a given function value.. 함수의 최대/최소값을 얻을 수 있는 인자 값을 찾아야 하는 경우 argmax/argmin이라는 기호를 사용한다. argument의 줄임이다.

출처 : light-tree.tistory.com/125  , www.clien.net/service/board/kin/5979004

---

Cascade of Pose Regressors

Cascade를 구현하기 위해서 먼저 예측된 좌표 주변으로 바운딩 박스를 그린다. 그리고 이 박스를 다시 CNN을 돌려 정교화된 좌표 예측 값을 구한다. 이러한 방법은 높은 해상도의 이미지를 보게 하여 높은 정밀도로 학습하게 한다.

 

 

s = 1 일 때, $b^{0}$는 전체 이미지이거나 person detector에 의해 얻어진 이미지이며, 이때 초기 pose는 다음과 같이 얻을 수 있다. 처음에는 모든 관절에 대해서 한번에 수행한다. 그 후 Stage에서는 i가 1~k로써 모든 관절에 대해서 각각 수행한다.

 

 

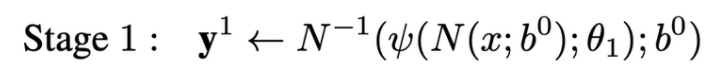
s≥2 인 후속 단계에서는 각 Stage 마다 다른 파라미터를 사용하기 때문에 각 Stage마다 동일한 학습을 해야한다. 각 Stage의 각 Joint는 각기 다른 BB에 의해 Normalization된다. 이때, 여기서 BB의 위치는 전 단계의 전처리된 변량 $y_i^{s} - y_i^{(s-1)}$(이전 단계 결과를 기반으로 다음 단계에서는 중심 좌표를 얼마나 옮겨야 하는가 추정)에 영향을 받는다. 

먼저 모든 좌표들에 대해서 새로운 바운딩 박스를 그린다. σdiam($y^{s}$)라는 수식에 의해서 크기가 결정되는데, diam($y^{s}$)란 이전에 예측한 좌표들에서 왼쪽 어깨와 오른쪽 엉덩이 좌표 간의 거리를 의미하며, σ는 이를 적당히 키워주는 파라미터입니다. 이렇게 구한 새로운 바운딩 박스로 다시 예측 하는 것을 s 단계 만큼 반복하는 것을 의미합니다.

 

 

N(x;b) : x에서 bounding box로 얻어진 정규화된 이미지 
ψ(N(x;b);θs) : 정규화된 부분 이미지에서 변량 추정 
$N^{-1}$(ψ(N(x;b);θs); b) : 추정된 변량을 절대적인 이미지 좌표로 변환

 

딥러닝 방법은 capacity(생산능력)이 매우 크기 때문에 각 이미지와 관절에 대해서 여러 normalization을 적용함으로써 학습 데이터는 증가한다. 그리고 이전 Stage 추정 결과만 사용하는 것이 아니라 simulated(모조의) 예측값을 이용한다. 이는 각 Stage, 각 Joint에 대해서 모든 학습 데이터의 displacement(차분 데이터)의 mean(평균)과 variance(분산)을 계산하여 2차 정규 분포 함수를 만든다. 즉, 해당 정규분포함수에 의해서 각  Stage, 각 Joint는 Normalzation될 수 있다. 즉, $y_i^{s} - y_i^{(s-1)}$← 정규분포 랜덤 벡터를 변위 벡터로 대체한다. Cascade 각 단계에서의 학습 목적함수는 아래와 같으며, 이때 $D_A^{s}$는 $D_N$과 달리 바운딩 박스로부터 cropping되는 영역의 데이터를 의미한다.

 

 

 

 

---

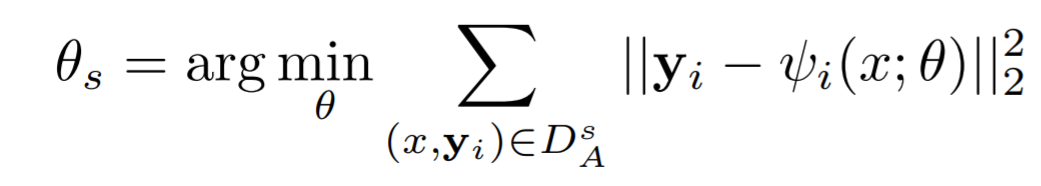
참고자료

영상 보행자 검출 기술(Pedestrian Detection) - 정보공유

[2014_CVPR] DeepPose: Human Pose Estimation via Deep Neural Networks

갈아먹는 Pose Estimation [1] DeepPose: Human Pose Estimation via Deep Neural Networks

Review: DeepPose — Cascade of CNN (Human Pose Estimation)

"Deep pose: Human Pose Estimation via Deep Neural Networks", 2014 CVPR