1. 기본적인 수학 연산
Numpy는 배열에 대한 기본적인 수학 연산을 지원합니다. 이 연산은 배열의 각 요소에 개별적으로 적용되며, 새 배열을 생성하여 결과를 반환합니다.
1.1 Addition (덧셈)
Numpy 배열에서 덧셈은 '+' 연산자 또는 'np.add() 함수를 사용하여 수행할 수 있습니다. 두 가지 방법 모두 배열 a와 b의 각 요소를 더한 결과인 [5, 7, 9]를 출력합니다.
import numpy as np
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
# Using '+'
print(a + b)
# Using np.add()
print(np.add(a, b))
# 출력: [5 7 9]

1.2 Subtraction (뺄셈)
Numpy에서 뺄셈은 - 연산자 또는 np.subtract() 함수를 사용합니다. 두 가지 방법 모두 배열 a에서 b를 뺀 결과인 [-3, -3, -3]를 출력합니다.
# Using '-'
print(a - b)
# Using np.subtract()
print(np.subtract(a, b))
# 출력: [-3 -3 -3]
1.3 Multiplication (곱셈)
Numpy에서 곱셈은 * 연산자 또는 np.multiply() 함수를 사용하여 수행합니다. 두 가지 방법 모두 곱셈을 수행하면, a와 b 배열의 각 요소를 곱한 결과인 [4, 10, 18]를 출력합니다.
# Using '*'
print("a * b = ", a * b)
# Using np.multiply()
print("a * b = ", np.multiply(a, b))
# 출력: [ 4 10 18]
1.4 Division (나눗셈)
Numpy에서 나눗셈은 / 연산자 또는 np.divide() 함수를 사용하여 수행합니다. 두 가지 방법 모두 나눗셈을 수행하면, a와 b 배열의 각 요소를 나눈 결과인 [0.25, 0.4 , 0.5 ]를 출력합니다.
# Using '/'
print("a / b = ", a / b)
# Using np.divide()
print("a / b = ", np.divide(a, b))
# 출력: [0.25 0.4 0.5 ]
1.5 Modulo Operation (나머지 연산)
Numpy에서 나머지 연산은 % 연산자 또는 np.mod() 함수를 사용하여 수행합니다. 나머지 연산을 수행하면, a와 b 배열의 각 요소를 나눈 나머지인 [1, 2, 3]를 출력합니다.
# Using '%'
print("a % b = ", a % b)
# Using np.mod()
print("a % b = ", np.mod(a, b))
# 출력: [1 2 3]
1.6 Exponentiation (지수)
Numpy의 np.exp() 함수를 사용하여 배열의 각 요소의 지수를 계산할 수 있습니다. 결과는 [2.71828183, 7.3890561 , 20.08553692]를 출력합니다.
print(np.exp(a)) # 출력: [ 2.71828183 7.3890561 20.08553692]
1.7 Square root (제곱근)
np.sqrt() 함수는 배열의 각 요소에 대해 제곱근을 계산합니다. 결과는 [1. , 1.41421356, 1.73205081]를 출력합니다.
print(np.sqrt(a)) # 출력: [1. 1.41421356 1.73205081]
2. Broadcasting (브로드캐스팅)
Numpy의 브로드캐스팅 기능은 서로 다른 크기의 배열에 대해 산술 연산을 수행하는 방법입니다. 이 기능을 통해 배열의 모양을 자동으로 조정하여 요소별 연산을 수행할 수 있습니다. 브로드캐스팅은 코드를 간결하게 만들고 컴퓨터의 처리 속도를 향상시킵니다.
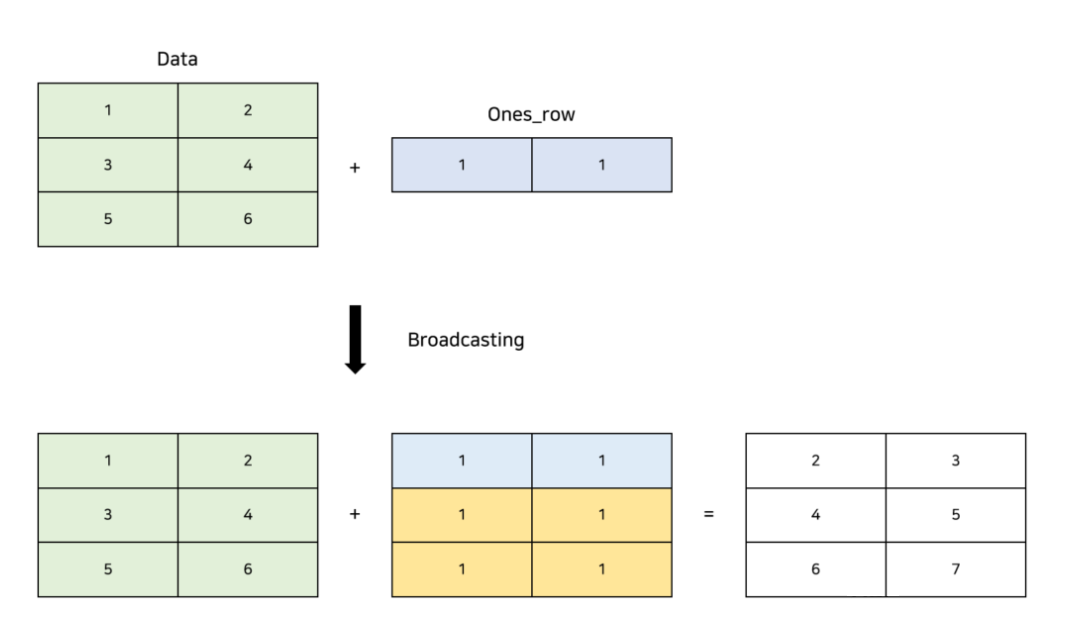
브로드캐스팅 규칙
- 두 배열의 차원 수가 다른 경우, 더 작은 수의 차원을 가진 배열의 형태(shape) 앞쪽을 1로 채웁니다.
- 예를 들어, 1차원 배열 [1, 2, 3]과 2차원 배열 [[1, 2, 3], [4, 5, 6]]이 있을 때, 1차원 배열이 실제로는 [[1, 2, 3]]처럼 2차원으로 변환된다는 의미입니다. 그래서 두 배열은 [[1, 2, 3], [4, 5, 6]] + [[1, 2, 3]] 형태로 계산되게 됩니다.
- 두 배열이 어떤 차원에서 크기가 일치하지 않는 경우, 해당 차원의 크기가 1인 배열이 다른 배열의 크기와 일치하도록 변형됩니다.
- 1차원 배열 [1, 2, 3]과 2차원 배열 [[1], [2]]가 있을 때, 1차원 배열이 실제로는 [[1, 2, 3], [1, 2, 3]]처럼 2차원으로 변환되고, 2차원 배열은 [[1, 1, 1], [2, 2, 2]]로 변형됩니다. 그래서 두 배열은 [[1, 1, 1], [2, 2, 2]] + [[1, 2, 3], [1, 2, 3]] 형태로 계산되게 됩니다.
- 두 배열이 브로드캐스팅으로 일치시킬 수 없는 경우, 즉 위의 규칙을 만족시키지 못하는 경우 에러가 발생합니다.
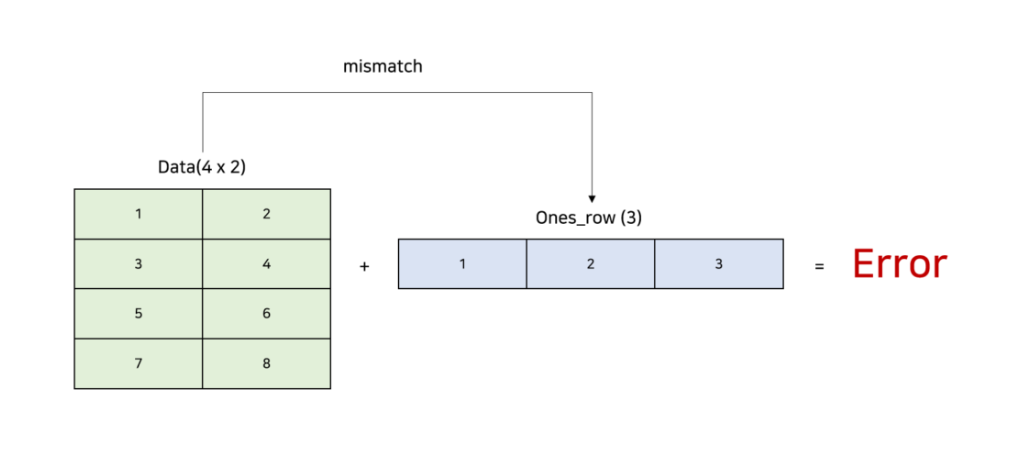
아래 코드에서 배열 a는 크기가 3이고, b는 스칼라 값입니다. 스칼라 값 b는 브로드캐스팅을 통해 배열 a와 동일한 크기로 확장되고, 각 요소는 원래 스칼라 값 b와 동일합니다. 그런 다음, 요소별 곱셈이 수행됩니다.
import numpy as np
a = np.array([1, 2, 3])
b = 2
print(a * b) # 출력: [2 4 6]
2.1 행이 많을 때의 브로드캐스팅
아래 코드에서 a는 3x3 크기의 2차원 배열이고, b는 크기가 3인 1차원 배열입니다. 브로드캐스팅 규칙에 따라, b 배열이 a 배열과 같은 크기인 (3, 3)으로 확장되어 각 행이 [1, 2, 3]가 됩니다. 그런 다음, 요소별 덧셈이 수행되어 위의 결과가 출력됩니다.
import numpy as np
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) # shape: (3, 3)
b = np.array([1, 2, 3]) # shape: (3,)
result = a + b
print(result)
#출력
#[[ 2 4 6]
# [ 5 7 9]
# [ 8 10 12]]
2.2 열이 많을 때의 브로드캐스팅
아래 코드에서 c는 3x1 크기의 2차원 배열이고, d는 크기가 3인 1차원 배열입니다. 브로드캐스팅 규칙에 따라, d 배열이 c 배열과 같은 크기인 (3, 3)으로 확장되어 각 열이 [1, 2, 3]이 됩니다. 그런 다음, 요소별 덧셈이 수행되어 위의 결과가 출력됩니다.
import numpy as np
c = np.array([[1], [2], [3]]) # shape: (3, 1)
d = np.array([1, 2, 3]) # shape: (3,)
result = c + d
print(result)
#출력
#[[2 3 4]
# [3 4 5]
# [4 5 6]]
3. 행렬 연산
3.1 행렬의 곱셈
Numpy는 요소별 곱셈(element-wise multiplication)과 행렬 곱셈(matrix multiplication)을 모두 지원합니다. * 연산자는 요소별 곱셈을 수행하며, np.dot() 함수나 @ 연산자는 행렬 곱셈을 수행합니다. 행렬 곱셈을 수행하려면 첫 번째 행렬의 열의 수와 두 번째 행렬의 행의 수가 같아야 합니다.
import numpy as np
A = np.array([[1, 2], [3, 4], [5, 6]])
B = np.array([[6, 5], [4, 3], [2, 1]])
print(A * B) # 요소별 곱셈
#출력 [[6 10] [12 12] [10 6]]
C = np.array([[1, 2], [3, 4]])
D = np.array([[5, 6], [7, 8]])
print(np.dot(C, D)) # 행렬 곱셈
#출력 [[19 22] [43 50]]
print(C @ D) # 행렬 곱셈
#출력 [[19 22] [43 50]]

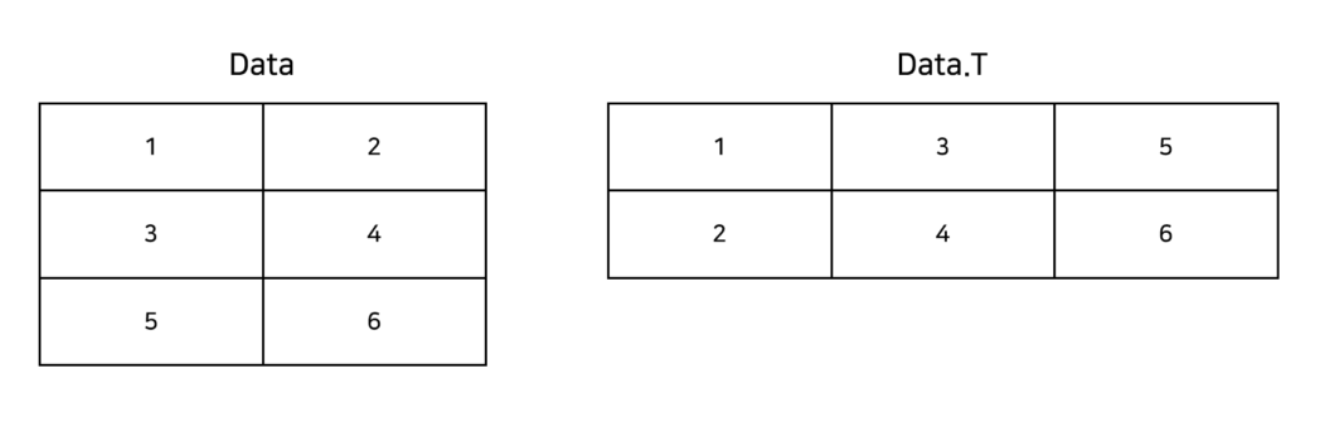
3.2 행렬의 전치
행렬의 전치는 행과 열을 바꾸는 연산입니다. Numpy의 np.transpose() 함수 또는 배열의 T 속성을 사용하여 행렬을 전치할 수 있습니다.
print(np.transpose(A)) #출력 [[1 3 5] [2 4 6]]
print(A.T) #출력 [[1 3 5] [2 4 6]]
3.3 행렬의 역행렬
Numpy의 np.linalg.inv() 함수를 사용하여 행렬의 역행렬을 계산할 수 있습니다. 이 함수는 주어진 행렬이 역행렬을 가질 수 있는 경우에만 사용해야 합니다. 참고로, 모든 행렬이 역행렬을 가지는 것은 아닙니다. 행렬이 역행렬을 가지려면, 그 행렬은 정방행렬이어야 하며, 그 행렬의 행렬식(determinant)이 0이 아니어야 합니다.
E = np.array([[1, 2], [3, 4]])
print(np.linalg.inv(E)) #출력 [[-2. 1. ] [ 1.5 -0.5]]
3.4 행렬의 행렬식
행렬의 행렬식은 np.linalg.det() 함수를 사용하여 계산할 수 있습니다. 행렬식은 행렬이 역행렬을 가질 수 있는지를 판단하는 데 사용될 수 있습니다.
print(np.linalg.det(E)) # -2.0000000000000004
3.5 행렬의 외적
외적은 벡터 곱셈의 한 형태로, 두 벡터의 외적 결과는 두 벡터가 형성하는 평면에 수직인 벡터입니다. Numpy에서는 np.cross() 함수를 사용하여 외적을 계산할 수 있습니다.
v1 = np.array([1, 2, 3])
v2 = np.array([4, 5, 6])
cross_product = np.cross(v1, v2)
print("Cross product: ", cross_product) # [-3 6 -3]
